What if there was a financial system that would eliminate the need for the federal government to go into debt, that would eliminate the need for the Federal Reserve, that would end the practice of fractional reserve banking and that would dethrone the big banks? Would you be in favor of such a system? A surprising new IMF research paper entitled “The Chicago Plan Revisited” by Jaromir Benes and Michael Kumhof is making waves in economic circles all over the globe. The paper suggests that the world would be much better off if we adopted a system where the banks did not create our money. So instead of a system where more money is only created when more debt is created, we would have a system of debt-free money that is created directly by national governments. There have been others that have suggested such a system before, but to have an IMF research paper actually recommend that such a system be adopted is a very big deal. At the moment, the world is experiencing the biggest debt crisis in human history, and this proposal is being described as a “radical solution” that could potentially remedy some of our largest financial problems. Unfortunately, apologists for the current system are already viciously attacking this new IMF paper, and of course the big banks would throw a major fit if such a system was ever to be seriously contemplated. That is why it is imperative that we educate people about how money really works. Our current system is in the process of collapsing and we desperately need to transition to a new one.
What if there was a financial system that would eliminate the need for the federal government to go into debt, that would eliminate the need for the Federal Reserve, that would end the practice of fractional reserve banking and that would dethrone the big banks? Would you be in favor of such a system? A surprising new IMF research paper entitled “The Chicago Plan Revisited” by Jaromir Benes and Michael Kumhof is making waves in economic circles all over the globe. The paper suggests that the world would be much better off if we adopted a system where the banks did not create our money. So instead of a system where more money is only created when more debt is created, we would have a system of debt-free money that is created directly by national governments. There have been others that have suggested such a system before, but to have an IMF research paper actually recommend that such a system be adopted is a very big deal. At the moment, the world is experiencing the biggest debt crisis in human history, and this proposal is being described as a “radical solution” that could potentially remedy some of our largest financial problems. Unfortunately, apologists for the current system are already viciously attacking this new IMF paper, and of course the big banks would throw a major fit if such a system was ever to be seriously contemplated. That is why it is imperative that we educate people about how money really works. Our current system is in the process of collapsing and we desperately need to transition to a new one.
One of the fundamental problems with our current financial system is that it is based on debt. Just take a look at the United States. The way our system works today, the vast majority of all money is “created” either when we borrow money or the government borrows money. Therefore, the creation of more money creates more debt. Under such a system, it should not be surprising that the total amount of debt in the United States is more than 30 times larger than it was just 40 years ago.
We don’t have to do things this way. There is a better alternative. National governments can directly issue debt-free currency into circulation. The following is a brief excerpt from the IMF report…
At the height of the Great Depression a number of leading U.S. economists advanced a proposal for monetary reform that became known as the Chicago Plan. It envisaged the separation of the monetary and credit functions of the banking system, by requiring 100% reserve backing for deposits. Irving Fisher (1936) claimed the following advantages for this plan: (1) Much better control of a major source of business cycle fluctuations, sudden increases and contractions of bank credit and of the supply of bank-created money. (2) Complete elimination of bank runs. (3) Dramatic reduction of the (net) public debt. (4) Dramatic reduction of private debt, as money creation no longer requires simultaneous debt creation. We study these claims by embedding a comprehensive and carefully calibrated model of the banking system in a DSGE model of the U.S. economy. We find support for all four of Fisher’s claims.
Why should banks be allowed to create money?
That is a very good question.
Why should sovereign governments ever have to borrow money from anyone?
That is another very good question.
Our current system is designed to enrich the bankers and get everyone else into debt.
And is that not exactly what has happened?
Taking the creation of money away from the bankers would have some tremendous advantages. A recent article by renowned financial journalist Ambrose Evans-Pritchard described some of these benefits…
One could slash private debt by 100pc of GDP, boost growth, stabilize prices, and dethrone bankers all at the same time. It could be done cleanly and painlessly, by legislative command, far more quickly than anybody imagined.
The conjuring trick is to replace our system of private bank-created money — roughly 97pc of the money supply — with state-created money. We return to the historical norm, before Charles II placed control of the money supply in private hands with the English Free Coinage Act of 1666.
Specifically, it means an assault on “fractional reserve banking”. If lenders are forced to put up 100pc reserve backing for deposits, they lose the exorbitant privilege of creating money out of thin air.
The nation regains sovereign control over the money supply. There are no more banks runs, and fewer boom-bust credit cycles.
So why don’t we go to such a system immediately?
Well, the transition to such a system would undoubtedly be a major shock to the global financial system, and most people try to avoid significant short-term pain even if there are tremendous long-term benefits.
More importantly, however, is that the bankers have a tremendous amount of power in our society today, and they would move heaven and earth to keep a debt-free monetary system from ever being implemented.
You see, the influence of the bankers is not just limited to the big banks. Our largest financial institutions (and the people who own them) also have large ownership stakes in the vast majority of the big Fortune 500 corporations. In essence, the big banks are at the very pinnacle of “the establishment” in the United States and in almost every other major country in the western world.
And the vast majority of all political campaigns are funded by “the establishment”. It takes an enormous amount of money to win campaigns these days, and most politicians are extremely hesitant to bite the hands of those that feed them.
So don’t expect any changes to happen overnight.
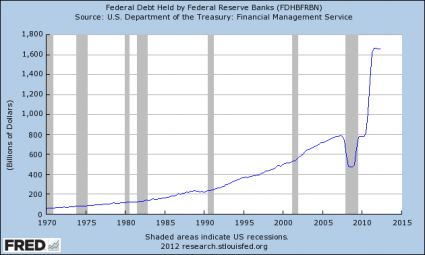
One proposal that has actually been put forward in Congress is to cancel all of the government debt that the Federal Reserve is currently holding. Right now, the Fed is holding more than 1.6 trillion dollars of U.S. government debt…
That would seem to make a lot of sense. That would immediately wipe more than 1.6 trillion dollars from the U.S. national debt without any real harm being done.
But “the establishment” would be horrified if such a thing happened, so I wouldn’t anticipate it happening any time soon.
Hopefully we can get the American people (along with people all over the globe) educated about these things so that we can start to get millions of people pushing for change.
A debt-free monetary system is superior to a debt-based monetary system in so many ways.
For example, if the U.S. government directly spent debt-free money into circulation, it could conceivably never need to borrow a single dollar ever again. If the government wanted to spend more money than it brought in, it would simply print it up and spend it.
Of course the big danger with that would be inflation. That is why it would be imperative for there to be a hard cap on what the government could spend. For example, you could set the cap on spending by the federal government at 20 percent of GDP. That way we would never end up looking like the Weimar Republic.
And the current federal debt could be paid down a little at a time using newly created debt-free dollars. This would have to be done slowly to keep inflation under control, but it could be done.
That way we would not hand a 16 trillion dollar debt to our children and our grandchildren. We created this mess so we should clean it up.
Theoretically you could also do away with the federal income tax if you wanted to. Personally, I would like to see the federal government be funded to a large degree by tariffs on foreign goods. That would also have the side benefit of bringing millions of jobs back into the United States.
Our system of income tax collection is just so incredibly inefficient. It costs us mind boggling amounts of time and money. Just consider the following stats from one of my previous articles…
1 – The U.S. tax code is now 3.8 million words long. If you took all of William Shakespeare’s works and collected them together, the entire collection would only be about 900,000 words long.
2 – According to the National Taxpayers Union, U.S. taxpayers spend more than 7.6 billion hours complying with federal tax requirements. Imagine what our society would look like if all that time was spent on more economically profitable activities.
3 – 75 years ago, the instructions for Form 1040 were two pages long. Today, they are 189 pages long.
4 – There have been 4,428 changes to the tax code over the last decade. It is incredibly costly to change tax software, tax manuals and tax instruction booklets for all of those changes.
5 – According to the National Taxpayers Union, the IRS currently has 1,999 different publications, forms, and instruction sheets that you can download from the IRS website.
6 – Our tax system has become so complicated that it is almost impossible to file your taxes correctly. For example, back in 1998 Money Magazine had 46 different tax professionals complete a tax return for a hypothetical household. All 46 of them came up with a different result.
7 – In 2009, PC World had five of the most popular tax preparation software websites prepare a tax return for a hypothetical household. All five of them came up with a different result.
8 – The IRS spends $2.45 for every $100 that it collects in taxes.
For long stretches of our history the United States did not have any income tax, and during those times we thrived. It is entirely conceivable that we could return to such a system.
At this point, the wealthy have become absolute masters at hiding their wealth from taxation. According to the IMF, a total of 18 trillion dollars is currently being hidden in offshore banks. What we are doing right now produces very inequitable results and it is not working.
In many ways, inflation would be a much fairer “tax” than the income tax because inflation taxes each dollar equally. Nobody would be able to cheat the system.
But if people really love the IRS and the federal income tax, we could keep them under a debt-free money system. I just happen to think that the IRS and the federal income tax are both really bad ideas that have never served the interests of the American people.
In any event, hopefully you can see that there is a much broader range of solutions to our problems than the two major political parties have been presenting to us.
We do not have to allow the banks to create our money.
The federal government does not have to go into more debt.
We don’t actually need the Federal Reserve.
There are alternatives to the federal income tax and the IRS.
Yes, it is very true that no system would be perfect. But clearly the path that we are on is only going to lead to disaster. U.S. government finances are a complete and total nightmare, and this mountain of debt that we have accumulated is going to absolutely destroy us if we allow it to.
So somebody out there should be proposing a fundamental change in direction for our financial system.
Unfortunately, our politicians are just proposing more of the same, and we all know where that is going to lead.